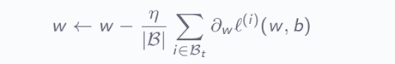1. A neural network (NN) can simply be seen as a series of different algorithms that aim to recognize patterns in the input data by processing information through different layers and neurons:
2. Linear Regression as a Neural Network
1. The model
2. The loss function
3. The optimization algorithm
4. The training function
3. 1 The Model: In the case of linear regression, the model is quite simple, and it simply encompasses 1 layer of neurons (each
corresponding to a different input) that are combined to form the output in the following linear way:
y = Xw + b
3.2 The loss function: A loss function to use in optimization problem with neural networks.This loss function will measure the fitness of the model (or better said, unfitness).
3.3 The optimization algorithm: main optimization technique most algorithms rely on stochastic gradient descent (SGD)
SGD reduces computational costs because the gradient is
computed from a uniform random sample of i examples in the data.
Update x, using a learning rate η as:
To increase speed- use minibatch SGD:
1. When updating the SGD algorithm, every observation takes time. Parsing the entire dataset for every update of the algorithm does as
well.
2. A faster intermediate strategy is taking a minibatch of observations, where weights are updated as:
4. The training: Training is the moment of the DL algorithm where we put all the other parts together.
▶ In each iteration, take a minibatch of examples to compute gradients and update model parameters.
▶ In each epoch, iterate through the entire training set.
- Initialize parameters → (w, b)
- Loop until max epochs or min error:
- Update gradients
- Update params
