Random World: Elementary Number Theory - The Theory of Congruences

1. Theorem 1: Let n be fixed positive integer. Two integers a and b are said to be congruent modulo n, symbolized by $a \equiv b (mod \: m)$

if n divides the difference a -b; that is provided that a-b = kn for some integer k. Example

$3 \equiv 24 (mod \: 7)$

2. Theorem 2: Let n > 1 be fixed and a, b, c, d be arbitrary integers. Then the following properties hold

(a) a $\equiv$ a (mod n)
(b) If a $\equiv$ b (mod n), then b $\equiv$ a (mod n)
(c) If a $\equiv$ b (mod n) and b $\equiv$ c (mod n), then a   $\equiv$ c (mod n)
(d) If a $\equiv$ b (mod n) and c $\equiv$ d (mod n), then a +c   $\equiv$ b + d (mod n) and ac $\equiv$ bd (mod n)
(e) If a $\equiv$ b (mod n), then a + c   $\equiv$ b + d (mod n) and ac $\equiv$ bd (mod n)
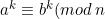(f) If a $\equiv$ b (mod n), then $a^k \equiv b ^k (mod\: n)$ for any positive integer k