Asset Price Volatility: The ARCH and GARCH Models
1. Financial time series, such as stock prices, interest rates, foreign exchange rates and inflation rates often exhibit the phenomenon of volatility clustering - that is, periods of turbulence in which their prices show wide swings and periods of tranquility in which there is relative calm
2. An average investor is not only concerned anout the rate of return, but also about the risk of investment as well as the variability, or volatility of risk.
3. A simple measure of asset return volatility is its variance over time. This also know as unconditional variance.
4. A measure that takes into account time-varying volatility is know as autoregressive conditional heteroscedasticity or ARCH for short.
5. How do we measure volatility ? ARCH model and its subsequent extensions attempt to answer this question Consider the simple linear regression model
the random variable 
is a function of the vatiable 
(or a vector of variables if there are more variables) and 
. Assume that ~ iid N (0,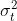
)
6. The error term is independently and identically normally distributed with mean 0 and variance of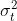, taking the ARCH into effect 
that is, we assume the error variance at time t is equal to some constant multiplied by the squared error term in the previous time period. If 
is zero, the error term is homoscedastic
7. ARCH (p) model:
8. ARCH effect can be tested by statistical significane of the estimated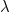
coefficients. Using a chi-square test
9. ARCH Estimation - Least squares method. Howeever this method has drawbacks -
1) They consume too many degrees of freedom (i.e. too many parameters need to be estimated)
2) There is no gurantee that all the estimated ARCH coefficeints will be positive
3) For the ARCH model we need to estimated both the mean and variance function simultaneously
10. ARCH Estimation - Maximum Likelihood Approach - One advantage is that the mean and variance can be estimated simultaneously, instead of separate as under OLS
11. Given the drawbacks of the ARCH (p) model - literature suggests that an ARCH model higher than ARCH (3) is better estimated by GARCH.
12. Simplest form of GARCH model
here the conditional variance at time t depends not only on the lagged squared error term at time t-1 but also on lagged variance term at time (t-1).
13. It can be shown that ARCH(p) model is equivalent to GARCH (1,1) as p increases.
14. GARCH-M model - Average investor is interested not only maximinzing the return, but also minimizing risk. The mean return can be modified to by explicitly introducing the risk factor, the conditional variance
. The risk factor is stastically significant, guggesting that not only is there an ARCH effect, but also that the mean return is directly affected by the risk factor.
15. Apart from the technical aspect of volatility, the topic is of pratical interest to investors at all levels, for an investor is not only interested in obtaining a higher rate of return, but also a steady (.i.e less volatile) rate of return.
1. Financial time series, such as stock prices, interest rates, foreign exchange rates and inflation rates often exhibit the phenomenon of volatility clustering - that is, periods of turbulence in which their prices show wide swings and periods of tranquility in which there is relative calm
2. An average investor is not only concerned anout the rate of return, but also about the risk of investment as well as the variability, or volatility of risk.
3. A simple measure of asset return volatility is its variance over time. This also know as unconditional variance.
4. A measure that takes into account time-varying volatility is know as autoregressive conditional heteroscedasticity or ARCH for short.
5. How do we measure volatility ? ARCH model and its subsequent extensions attempt to answer this question Consider the simple linear regression model
6. The error term is independently and identically normally distributed with mean 0 and variance of
7. ARCH (p) model:
8. ARCH effect can be tested by statistical significane of the estimated
9. ARCH Estimation - Least squares method. Howeever this method has drawbacks -
1) They consume too many degrees of freedom (i.e. too many parameters need to be estimated)
2) There is no gurantee that all the estimated ARCH coefficeints will be positive
3) For the ARCH model we need to estimated both the mean and variance function simultaneously
10. ARCH Estimation - Maximum Likelihood Approach - One advantage is that the mean and variance can be estimated simultaneously, instead of separate as under OLS
11. Given the drawbacks of the ARCH (p) model - literature suggests that an ARCH model higher than ARCH (3) is better estimated by GARCH.
12. Simplest form of GARCH model
13. It can be shown that ARCH(p) model is equivalent to GARCH (1,1) as p increases.
14. GARCH-M model - Average investor is interested not only maximinzing the return, but also minimizing risk. The mean return can be modified to by explicitly introducing the risk factor, the conditional variance
15. Apart from the technical aspect of volatility, the topic is of pratical interest to investors at all levels, for an investor is not only interested in obtaining a higher rate of return, but also a steady (.i.e less volatile) rate of return.