Introduction, Vector Functions and Electrostatics
1. In this text the subject of vector calculus is presented in the context of simple electrostatics
2. We follow this procedure for two reasons 1) vector calculus was invented for use in electromagnetic theory and is ideally suited to it 2) some mathematics is best discussed in a context which is not exclusively mathematical
Vector Functions
1. An electric field is an example of what we call a vector function.
2. A vector function (in three dimensions) is a rule which tells us how to associate a vector with each point (x, y, z). An example is the velocity of a fluid. Designating this function V (x, y, z) it specifies the speed of the fluid as well the direction of flow at the point (x, y, z). An example is the velocity of the fluid.
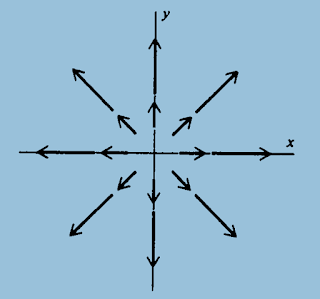
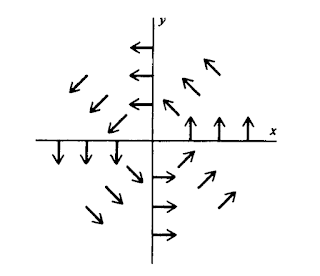
3. We can picture a vector function as collection of arrows
&space;\mathbf{\bar{u}} "\mathbf{F} = \frac{1}{4\pi \epsilon } (\frac{qq_0}{r^2}) \mathbf{\bar{u}}")
where 
is a unit vector pointing from 
to 
, and K is constant of proportionality
1. In this text the subject of vector calculus is presented in the context of simple electrostatics
2. We follow this procedure for two reasons 1) vector calculus was invented for use in electromagnetic theory and is ideally suited to it 2) some mathematics is best discussed in a context which is not exclusively mathematical
Vector Functions
1. An electric field is an example of what we call a vector function.
2. A vector function (in three dimensions) is a rule which tells us how to associate a vector with each point (x, y, z). An example is the velocity of a fluid. Designating this function V (x, y, z) it specifies the speed of the fluid as well the direction of flow at the point (x, y, z). An example is the velocity of the fluid.
3. We can picture a vector function as collection of arrows
4. A vector function, like a vector, can be resolved into components - i, j, k
5. An example of a vector function F(x, y) = ix + iy
you probably recognize this function as the position vector r
A second example &space;=&space;\frac{-iy&space;+&space;jx}{\sqrt{x^2+y^2}} "\mathbf{G}(x,y) = \frac{-iy + jx}{\sqrt{x^2+y^2}}")
. The vector field is shown in the figure
6. Electrostatic field E(r) = F (r)/q o, where F(r) =
This electrostatic field at r = ix+ jy + kz is produced by charges qi at ri ( i = 1, 2, 3, .. N). The above equation says that the field due to a group of charges is the vector sum of the fields each produces alone.
7. In electrostatics we are interested in the effect that a given set of charges produces on another set. The problem can be conveniently divided into two parts by introducing the electrostatic field, for then we can (a) calculate the field due to a given distribution of charges without worrying about the effect these charges have on other charges in the vicinity (b) calculate the effect a given field has on charges placed in it without worrying about the distribution of charges that produced the field. This book concerns with (a)
8. All classical electromagetic theory can be codified in terms of four equations, called Maxwell's equations, which relates fields (electric and magnetic) to each other.
9. Electromagnetism is a field theory and the electric field ultimately plays a role and assumes an importance which far transcends its elementary definition as "force per unit charge"